Roy Research Group

Overview of Driven Quantum Systems


Fig: Schematic representation of a Thouless pump	The introduction of time dependence into a quantum system can dramatically increase the complexity of the problem. In such dynamical systems, traditional concepts from equilibrium physics, such has the notion of a ground state, are no longer useful. Instead, an understanding of these systems—and even the notion of a ‘phase’ away from equilibrium— requires fundamentally different theoretical approaches. On the other hand, dynamical systems offer the chance to generate exotic new phases that cannot exist in static systems. Many such phases are directly accessible in the laboratory—where lasers and modulated electromagnetic fields may be used to drive a system out of equilibrium.

Fig: Schematic representation of a Thouless pump

The introduction of time dependence into a quantum system can dramatically increase the complexity of the problem. In such dynamical systems, traditional concepts from equilibrium physics, such has the notion of a ground state, are no longer useful. Instead, an understanding of these systems—and even the notion of a ‘phase’ away from equilibrium— requires fundamentally different theoretical approaches. On the other hand, dynamical systems offer the chance to generate exotic new phases that cannot exist in static systems. Many such phases are directly accessible in the laboratory—where lasers and modulated electromagnetic fields may be used to drive a system out of equilibrium.


There has recently been much theoretical and experimental interest in quantum systems that are driven periodically in time, known as Floquet systems [1-2]. In these cases, fast oscillations can be used to alter the underlying band structure of the static (or time-averaged) system, generating exotic topological phases through a form of band structure engineering [1-2]. This has recently been demonstrated in the laboratory using both photonic systems and ultracold atomic gases [3–6]. Most interestingly, dynamical analogues of topological insulators and superconductors have been predicted that would be impossible to realise in a static system (see [7–8] for a complete list of references). Our group is interested in a range of open questions that arise in driven systems, with a particular focus on the exotic topological phases that can exist only in dynamical systems. We recently uncovered a number of new examples of such driven topological phases. We also unified previously discovered driven topological phases in a periodic table of dynamical topological insulators and superconductors, which rigorously classifies all topological phases of free fermions in any number of dimensions [8]. In the presence of interactions and symmetry, dynamical analogues of symmetry protected topological phases (SPTs) had also been predicted to arise [9], with many-body localization (MBL) a crucial ingredient. We were one of a number of groups who provided a complete classification of a set of such phases in one dimension [10]. We are actively pursuing further ideas at this interface between symmetry, topology, interactions and time dependence, where many unsolved problems remain.

There has recently been much theoretical and experimental interest in quantum systems that are driven periodically in time, known as Floquet systems [1-2]. In these cases, fast oscillations can be used to alter the underlying band structure of the static (or time-averaged) system, generating exotic topological phases through a form of band structure engineering [1-2]. This has recently been demonstrated in the laboratory using both photonic systems and ultracold atomic gases [3–6]. Most interestingly, dynamical analogues of topological insulators and superconductors have been predicted that would be impossible to realise in a static system (see [7–8] for a complete list of references).

Our group is interested in a range of open questions that arise in driven systems, with a particular focus on the exotic topological phases that can exist only in dynamical systems. We recently uncovered a number of new examples of such driven topological phases. We also unified previously discovered driven topological phases in a periodic table of dynamical topological insulators and superconductors, which rigorously classifies all topological phases of free fermions in any number of dimensions [8].

In the presence of interactions and symmetry, dynamical analogues of symmetry protected topological phases (SPTs) had also been predicted to arise [9], with many-body localization (MBL) a crucial ingredient. We were one of a number of groups who provided a complete classification of a set of such phases in one dimension [10]. We are actively pursuing further ideas at this interface between symmetry, topology, interactions and time dependence, where many unsolved problems remain.

Topological Phases of Free Fermions in Floquet Systems


Fig: Decomposition of a unitary evolution into loop and constant components	A central principle that arises in the study of topological insulators is holography: the idea that the properties of a bulk topological phase are manifested on the boundaries of the system. This bulk-edge correspondence is neatly summarised in the celebrated periodic table of topological insulators and superconductors (TIs) [11], which classifies the bulk invariants (and associated edge modes) that may exist in a topological phase of free fermions. Notably, the edge modes of a TI in d dimensions are anomalous: the Hamiltonian that describes the physics at the boundary cannot be generated in a d-1 dimensional system. In [8] we investigated similar holographic principles in driven systems of free fermions, uncovering several new driven topological phases and unifying previous work in this field. In a periodically driven system, the time evolution is described by a unitary operator, which derives from the underlying time-dependent Hamiltonian. In such systems, the energy of a state is no longer well defined, and states are instead labelled by a complex phase known as the quasienergy. Eigenstates, and their associated properties, may only be defined stroboscopically.

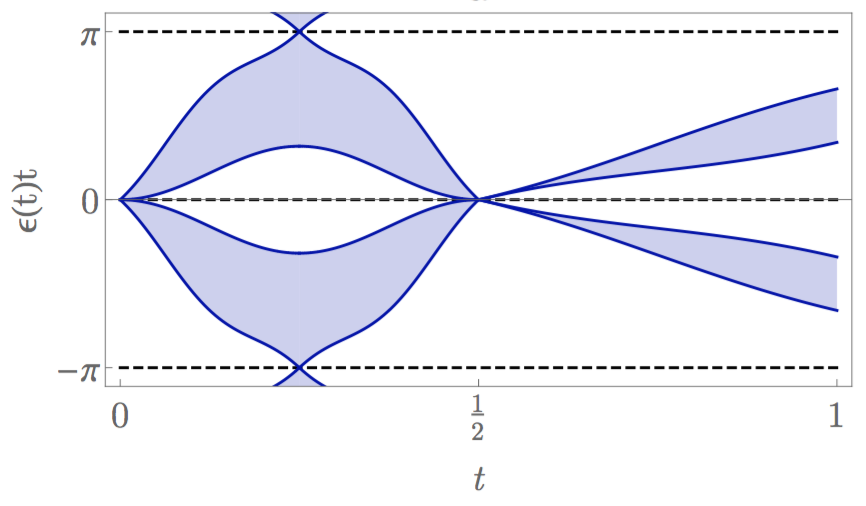Fig: Decomposition of a unitary evolution into loop and constant components

A central principle that arises in the study of topological insulators is holography: the idea that the properties of a bulk topological phase are manifested on the boundaries of the system. This bulk-edge correspondence is neatly summarised in the celebrated periodic table of topological insulators and superconductors (TIs) [11], which classifies the bulk invariants (and associated edge modes) that may exist in a topological phase of free fermions. Notably, the edge modes of a TI in d dimensions are anomalous: the Hamiltonian that describes the physics at the boundary cannot be generated in a d-1 dimensional system. In [8] we investigated similar holographic principles in driven systems of free fermions, uncovering several new driven topological phases and unifying previous work in this field.

In a periodically driven system, the time evolution is described by a unitary operator, which derives from the underlying time-dependent Hamiltonian. In such systems, the energy of a state is no longer well defined, and states are instead labelled by a complex phase known as the quasienergy. Eigenstates, and their associated properties, may only be defined stroboscopically.

Studies of time-dependent free-fermion systems have demonstrated the existence of edge modes that are qualitatively different from the edge modes in static TIs, such as Majorana and chiral modes at quasienergy Pi [12-15]. In these cases, the dynamical edge modes of a d-dimensional system correspond to the anomalous action of the unitary operator at the boundary, which could not arise from evolving a d-1 dimensional system.

Motivated by discussions with Ben Fregoso and Shivaji Sondhi, my coworkers and I generalized this bulk-boundary correspondence to all unitary evolutions in any dimension [8], uncovering several new dynamical topological phases in the process. We used a variant of the K-theory methods originally used by Kitaev to classify static TIs [11]. This marked a novel use of K-theory methods, which had previously only been used to classify Hamiltonians, rather than unitaries. Inspired by discussions with Graeme Segal, we mapped sets of unitaries onto sets of Hermitian maps that involved new symmetries and a new time variable. Then, with a suitable definition of stable homotopy, we constructed additive categories for each symmetry class from these Hermitian maps. This enabled us to define a K-theory in terms of quasi-surjective Banach functors between pairs of additive categories [16-17]. Finally, using the Morita equivalence of these categories, we showed that the classification of unitaries reduces to a form similar to the classification of static TIs.

We found that unitary evolutions have a twofold classification, as shown in the table below. Note that this table contains within it the periodic table of static TIs, which simply correspond to unitary evolutions with a constant Hamiltonian.

Fig: Classification of two-gapped unitaries by symmetry class and spatial dimension d. The table repeats for d ≥ 8 (Bott periodicity)

Symmetry Protected Topological phases (SPTs) in Floquet Systems

In the presence of both symmetry and interactions, a rich set of topological states, known as symmetry protected topological phases (SPTs), is known to exist. A complete classification of these systems has not yet been obtained, but rigorous results exist for static bosonic systems in one to three dimensions [18]. A natural question to ask is how this classification changes if we allow the system to vary with time. Are there new phases that are inherently dynamical in nature? Early work in this direction suggested that this is indeed the case [9]. The new driven phases of free fermionic systems [8] and some early work on interacting systems [9] suggested that this is indeed the case.

Motivated by discussions with Curt von Keyserlingk and Shivaji Sondhi, our group was one of a number of groups [10,19–21] to provide a complete classification of time-dependent Abelian SPT phases in one dimension. Using intuition developed from the study of Floquet systems in Class D, we showed how to construct nontrivial dynamical SPT phases for an arbitrary Abelian symmetry group. This requires the construction of nontrivial unitary cycles, which may be obtained by evolving first with a trivial Hamiltonian and then with a nontrivial Hamiltonian. Uniquely, our work provides an explicit bulk-boundary correspondence for such dynamical SPT phases and describes how to calculate topological invariants in each case.

For class D, the free fermion classification is unchanged upon the introduction of interactions, in a similar way to interacting static systems in class D [22]. A topological invariant may be constructed by inserting a flux into the system throughout the evolution, and this nontrivial topology has specific signatures in the many-body quasienergy spectrum (see figure). This is reminiscent of the topological invariant defined by Kitaev for the SPT phases in one dimension in this class [Kitaev 2001].

To generate dynamical bosonic SPT phases, we constructed nontrivial unitary cycles from the SPT models of Ref. [23]. In these systems, dynamical SPT phases correspond to irreducible representations of the symmetry group, while topological invariants may be constructed by applying twisted boundary conditions. These results generalise to all Abelian symmetry groups, providing a complete classification of such phases.

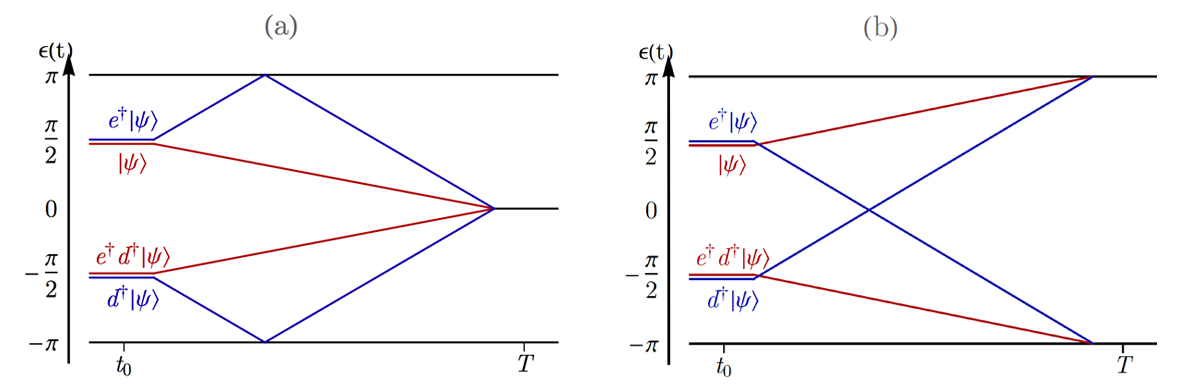
Fig: Schematic splitting of a Majorana multiplet at a (0,π)-phase transition as the system is closed with (a) periodic and (b) antiperiodic boundary conditions.


Fig: Schematic representation of an adiabatic cycle*	Adiabatic Cycles In contrast to Floquet systems, where driving occurs at a single, often high, frequency, we can also consider the slow evolution of a system over one complete cycle. An adiabatic cycle is an evolution of this kind that maintains any bulk gaps that are present in the initial Hamiltonian. Even under these simplifying assumptions, Thouless showed that nontrivial physics can arise when the cycle is completed [24]—for example, a nontrivial Berry phase may be picked up, corresponding to a pumped unit of charge. In the presence of symmetries, preserved throughout the evolution, adiabatic cycles may have more general effects. In Ref. [25] we studied adiabatic cycles in the ten AZ symmetry classes in all dimensions and uncovered a number of new, interesting types of pump in one and higher dimensions.

Fig: Schematic representation* of an adiabatic cycle

Adiabatic Cycles

In contrast to Floquet systems, where driving occurs at a single, often high, frequency, we can also consider the slow evolution of a system over one complete cycle. An adiabatic cycle is an evolution of this kind that maintains any bulk gaps that are present in the initial Hamiltonian. Even under these simplifying assumptions, Thouless showed that nontrivial physics can arise when the cycle is completed [24]—for example, a nontrivial Berry phase may be picked up, corresponding to a pumped unit of charge. In the presence of symmetries, preserved throughout the evolution, adiabatic cycles may have more general effects. In Ref. [25] we studied adiabatic cycles in the ten AZ symmetry classes in all dimensions and uncovered a number of new, interesting types of pump in one and higher dimensions.

References

[1] J. Cayssol, B. Do ́ra, F. Simon, and R. Moessner, Phys. Status Solidi RRL 7, 101 (2013).
[2] M. Bukov, L. D’Alessio, and A. Polkovnikov, Adv. Phys. 64, 139 (2015).
[3] M. C. Rechtsman et al., Nature 496, 196 (2013).
[4] T. Kitagawa, M. A. Broome, A. Fedrizzi, and M. S. Rudner, Nat. Commun. 3, 882 (2012).
[5] G. Jotzu, M. Messer, R. Desbuquois, M. Lebrat, T. Uehlinger, D. Greif, and T. Esslinger, Nature 515, 237 (2015).
[6] K. Jiménez-García et al., Phys. Rev. Lett. 114, 125301 (2015).
[7] F. Nathan and M. S. Rudner, New Journal of Physics 17, 125014 (2015).
[8] R. Roy and F. Harper, arXiv:1603.06944 (2016).
[9] V. Khemani, A. Lazarides, R. Moessner, and S. L. Sondhi, Phys. Rev. Lett. 116, 250401.
[10] R. Roy and F. Harper, arXiv:1602.08089 (2016).
[11] A. Kitaev, in AIP Conference Proceedings (2009) pp. 22–30.
[12] T. Kitagawa, E. Berg, M. Rudner, and E. Demler, Phys. Rev. B 82, 235114 (2010).
[13] L. Jiang et al., Phys. Rev. Lett. 106, 220402 (2011).
[14] M. S. Rudner, N. H. Lindner, E. Berg, and M. Levin, Phys. Rev. X 3, 031005 (2013).
[15] M. Thakurathi, A. A. Patel, D. Sen, and A. Dutta, Phys. Rev. B 88, 155133 (2013).
[16] M. F. Atiyah, K-Theory (Benjamin, New York, NY, 1967).
[17] M. Karoubi, K-Theory: An Introduction, Classics in mathematics (Springer, Berlin, 1978).
[18] X. Chen, Z.-C. Gu, Z.-X. Liu, and X.-G. Wen, Phys. Rev. B 87, 155114 (2013).
[19] C. W. von Keyserlingk and S. L. Sondhi, Phys. Rev. B 93, 245145 (2016).
[20] D. V. Else and C. Nayak, Phys. Rev. B 93, 201103(R) (2016).
[21] A. C. Potter, T. Morimoto, and A. Vishwanath, arXiv 1602.05194v1 (2016).
[22] L. Fidkowski, and A. Kitaev, Phys. Rev. B, 81 134509 (2010).
[23] S. D. Geraedts and O. I. Motrunich, arXiv:1410.1580 (2014).
[24] D. J. Thouless, (1983). Phys. Rev. B 27, 6083 (1983).
[25] R. Roy, arXiv:1104.1979 (2011).