Localization and Topology in low dimensions
In one and two dimensional systems, electrons generically tend to localize in the presence of disorder. In topological phases, however complete localization is prevented. This dichotomy between localization and topology manifests in many different ways. In our group, we have been exploring some of these through the study of delocalization transitions in Floquet systems, properties of localized Wannier functions and the topological obstructions to creating them. Some of our recent work is described below.
Scattering Expansion for Localization in One Dimension
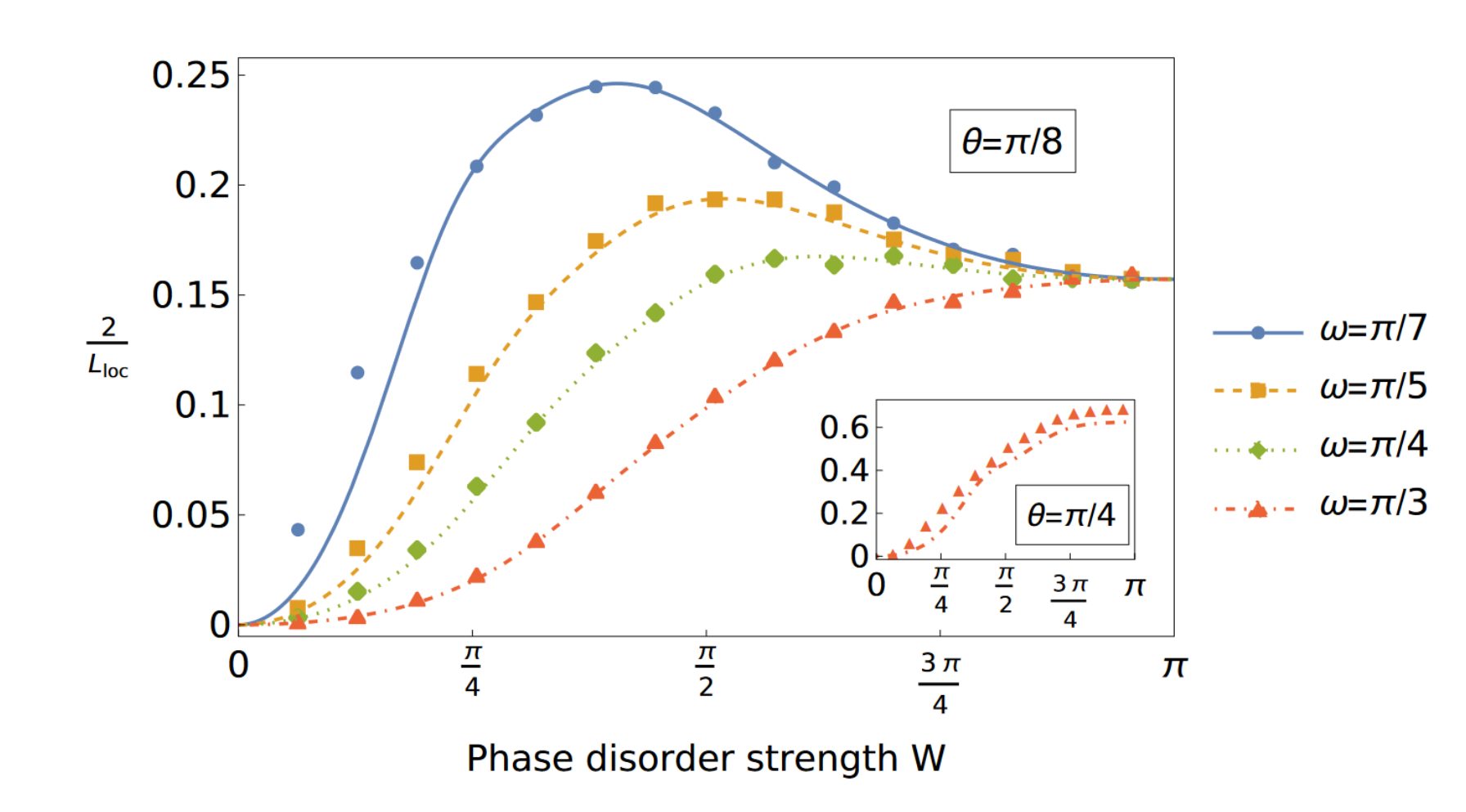
We present a perturbative approach to a broad class of disordered systems in one spatial dimension. Considering a long chain of identically disordered scatterers, we expand in the reflection strength of any individual scatterer. This expansion accesses the full range of phase disorder from weak to strong. As an example application, we show analytically that in a discrete-time quantum walk, the localization length can depend non-monotonically on the strength of phase disorder (whereas expanding in weak disorder yields monotonic decrease). Returning to the general case, we obtain to all orders in the expansion a particular non-separable form for the joint probability distribution of the log-transmission and reflection phase. Furthermore, we show that for weak local reflection strength, a version of the scaling theory of localizatioz holds: the joint distribution is determined by just three parameters.
Publications:
- Adrian B. Culver, Pratik Sathe and Rahul Roy. “Scattering Expansion for Localization in One Dimension.” (2022). [link][PDF]
Universal Delocalization Transition in Chiral Floquet Topological Insulators
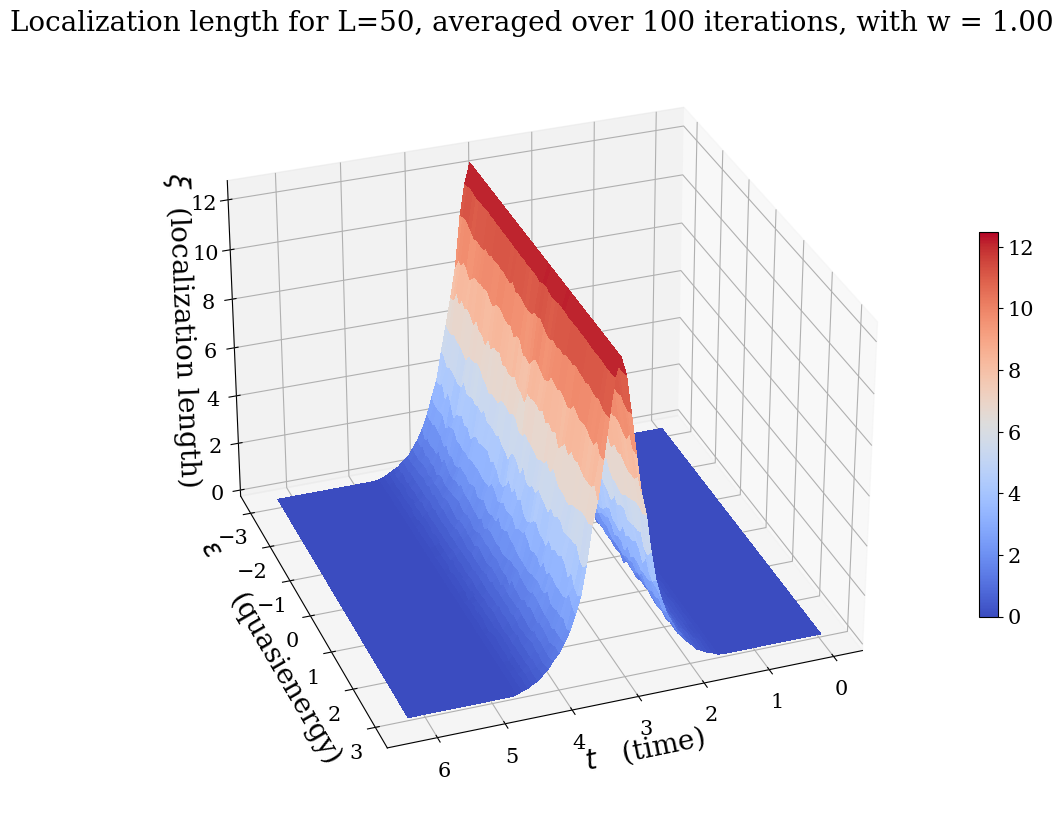
Periodically driven (Floquet) systems often exhibit behavior distinct from undriven systems. Any amount of disorder in one-dimensional undriven systems generically localizes all eigenstates. In contrast, we show that in topologically non-trivial, non-interacting Floquet loop drives with chiral symmetry, a delocalization transition occurs at as the time \(t\) is varied within the driving period (\(0< t< T_{drive}\)). We find that the localization length L loc at all quasienergies diverges with a universal exponent of \(2\) as \(t\) approaches the midpoint of the drive: \(L_{loc}~(t-T_{drive}/2)-2\). We provide numerical evidence for the universality of this exponent by studying a variety of such drives using exact diagonalization, and we also present an analytical argument based on scattering theory.
Compactly Supported Wannier Functions
Wannier functions that are maximally localized help in understanding many properties of crystalline materials. In the absence of topological obstructions, they are at least exponentially localized. In some cases such as flat-band Hamiltonians, it is possible to construct Wannier functions that are even more localized, so that they are compactly supported thus having zero support outside their corresponding locations. Under what general conditions is it possible to construct compactly supported Wannier functions? We answer this question in this paper. Specifically, we show that in 1d non-interacting tight-binding models, strict locality of the projection operator is a necessary and sufficient condition for a subspace to be spanned by a compactly supported orthogonal basis, independent of lattice translation symmetry. For any strictly local projector, we provide a procedure for obtaining such a basis. For higher dimensional systems, we discuss some additional conditions under which an occupied subspace is spanned by a compactly supported orthogonal basis, and show that the corresponding projectors are topologically trivial in many cases. We also show that a projector in arbitrary dimensions is strictly local if and only if for any chosen axis, its image is spanned by hybrid Wannier functions that are compactly supported along that axis.
Publications: